What Everybody Ought To Know About What Is The Kirchhoff Rule

Understanding Kirchhoff's Laws

1. What Are These "Laws" Anyway?

Ever wonder how electrical circuits work their magic? It's not just electrons randomly zooming around, you know! There are rules, fundamental principles, that govern their behavior. Enter Kirchhoff's Laws — the unsung heroes of circuit analysis. Think of them as the traffic cops directing the flow of electrons, ensuring everything runs smoothly and predictably. They're named after Gustav Kirchhoff, a brilliant German physicist who probably had a lot more fun with circuits than most of us.

Specifically, we're talking about two key laws: Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL). Don't let the names intimidate you. They're really quite intuitive once you grasp the basic concepts. Imagine KCL as the conservation of water flowing through a pipe system. What goes in must come out, right? And KVL? Think of it as an energy audit for a circuit loop. The total voltage increases have to equal the total voltage decreases. Simple, right?

Why are these laws so important? Well, without them, designing and troubleshooting electrical circuits would be like trying to build a house without a blueprint. You'd be guessing and hoping for the best, which, let's be honest, is rarely the best approach when dealing with electricity. Kirchhoff's laws provide a systematic way to analyze complex circuits, calculate currents and voltages, and ensure everything works as intended. They're the foundation upon which much of electrical engineering is built.

So, whether you're a budding electrician, a curious tinkerer, or just someone who wants to understand the world around them a little better, understanding Kirchhoff's Laws is a worthwhile endeavor. They're not just some abstract concepts confined to textbooks; they're practical tools that can help you solve real-world problems. And who knows, maybe one day you'll be the one designing the next groundbreaking electronic gadget, all thanks to good old Gustav and his laws!

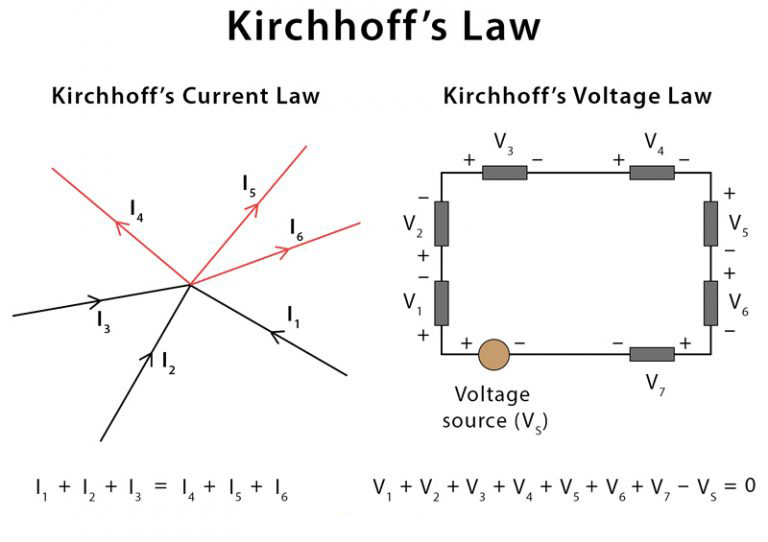
Kirchhoff's Current Law (KCL)

2. Current In = Current Out

Alright, let's dive into the first law: Kirchhoff's Current Law (KCL), sometimes affectionately referred to as the "node rule." At its core, KCL states that the algebraic sum of currents entering and leaving any node (a junction where two or more circuit elements meet) must be equal to zero. Put more simply, the total current flowing into a node is equal to the total current flowing out of that node. It's like a revolving door; the number of people entering must equal the number of people leaving (unless someone's decided to sneak out the back).

Think of it this way: electrons don't just vanish into thin air, nor do they magically appear from nowhere. They have to go somewhere. If current is flowing into a node through one wire, it must flow out of that node through another wire (or wires). The amount of current entering has to precisely match the amount leaving. This is because of the conservation of charge, one of the fundamental principles of physics. So, next time you see a node in a circuit diagram, remember the electron conservation act is in full effect!

Mathematically, KCL can be expressed as: Iin = Iout, where Iin is the sum of currents entering the node and Iout is the sum of currents leaving the node. You might also see it written as I = 0, where I is the sum of all currents (entering and leaving) the node, with currents entering assigned a positive sign and currents leaving assigned a negative sign (or vice versa, as long as you're consistent). Don't let the fancy symbols scare you; it's just a compact way of saying the same thing.

KCL is incredibly useful for analyzing circuits because it allows you to relate the currents in different branches of the circuit. If you know the currents in some branches, you can use KCL to find the currents in other branches. It's like having a hidden key that unlocks the secrets of the circuit. So, master this law, and you'll be well on your way to becoming a circuit-solving whiz!

Kirchhoff's Voltage Law (KVL)

3. Around the Loop, Voltage Adds Up to Zero

Now let's tackle the second law: Kirchhoff's Voltage Law (KVL), also known as the "loop rule." KVL states that the algebraic sum of all the voltages around any closed loop in a circuit must be equal to zero. Think of it like taking a hike up a mountain and back down. The total elevation gain must equal the total elevation loss, bringing you back to where you started. In a circuit, voltage represents the electrical potential energy, and KVL is saying that as you travel around a closed loop, all the energy gained from voltage sources must be used up by voltage drops across circuit elements like resistors.

Imagine a simple circuit with a battery and a resistor. The battery provides a voltage "gain," pushing electrons around the circuit. As the electrons flow through the resistor, they encounter resistance, which causes a voltage "drop." KVL tells us that the voltage drop across the resistor must be equal to the voltage gain provided by the battery. If it weren't, we'd be violating the law of conservation of energy, which, as you might imagine, is frowned upon by the laws of physics.

Mathematically, KVL can be expressed as: V = 0, where V is the sum of all the voltages (voltage gains and voltage drops) around the loop. Voltage gains are typically assigned a positive sign, and voltage drops are assigned a negative sign (again, consistency is key). This equation simply means that as you traverse the loop, adding up all the voltage rises and drops, you should end up back where you started, with a net change in voltage of zero.

KVL is an indispensable tool for analyzing circuits, especially those with multiple loops and branches. It allows you to write equations relating the voltages in different parts of the circuit, which can then be solved to find unknown voltages. It's like having a detailed map of the circuit's energy landscape, allowing you to navigate even the most complex paths. So, embrace the loop, master KVL, and you'll be well-equipped to conquer any circuit challenge!

Applying Kirchhoff's Laws in Practice

4. Putting Theory into Action

Okay, we've covered the theory behind Kirchhoff's Laws, but how do you actually use them to solve real-world circuit problems? Well, it's all about applying a systematic approach. First, identify the nodes and loops in the circuit. A node is simply a point where two or more circuit elements connect, and a loop is any closed path in the circuit.

Next, assign current variables to each branch of the circuit and voltage variables to each circuit element. Don't worry if you don't know the actual values of the currents and voltages yet; you're just giving them names so you can work with them. It's like labeling the ingredients in a recipe before you start cooking.

Then, apply KCL to each node in the circuit, writing equations that relate the currents entering and leaving each node. Similarly, apply KVL to each loop in the circuit, writing equations that relate the voltages around each loop. Remember to be consistent with your sign conventions (i.e., whether you assign positive or negative signs to currents entering or leaving a node, and to voltage gains or voltage drops around a loop).

Finally, solve the resulting system of equations to find the unknown currents and voltages. This may involve using algebraic techniques like substitution, elimination, or matrix methods. Don't be afraid to use a calculator or computer software to help you with the math. Once you've solved for the currents and voltages, you can use them to calculate other circuit parameters, such as power dissipation or resistance. With a little practice, you'll be solving circuit puzzles like a pro!

Beyond the Basics

5. More Than Just Simple Circuits

While Kirchhoff's Laws are fundamental principles, their application extends far beyond simple circuits. They form the basis for analyzing complex networks, including those found in power grids, communication systems, and electronic devices. Understanding these laws is crucial for engineers and technicians working in these fields.

One important consideration is the limitations of Kirchhoff's Laws. They are based on the assumption that the circuit elements are "lumped," meaning that their physical dimensions are much smaller than the wavelength of the signals propagating through them. In high-frequency circuits, this assumption may not hold, and more advanced techniques, such as transmission line theory, may be needed.

Furthermore, Kirchhoff's Laws are applicable only to linear circuits, where the voltage and current relationships are linear. In nonlinear circuits, such as those containing diodes or transistors, the analysis becomes more complex and may require the use of computer simulation tools.

Despite these limitations, Kirchhoff's Laws remain an essential tool for circuit analysis. They provide a solid foundation for understanding the behavior of electrical circuits and are used extensively in engineering design and analysis. So, keep practicing, keep exploring, and keep pushing the boundaries of what's possible with the power of electricity!

FAQs About Kirchhoff's Laws

6. Your Burning Questions Answered

Still scratching your head? Here are some frequently asked questions about Kirchhoff's Laws to help clear things up:

Q: What's the difference between KCL and KVL?

A: KCL deals with currents at a node, stating that the total current entering equals the total current leaving. KVL deals with voltages around a loop, stating that the sum of all voltages in a loop equals zero. Think of KCL as the "node rule" and KVL as the "loop rule."

Q: Do I need to know calculus to understand Kirchhoff's Laws?

A: Nope! Basic algebra is all you need to apply Kirchhoff's Laws to solve most circuit problems. While calculus might be used in more advanced circuit analysis, it's not necessary for understanding the fundamental concepts.

Q: Can I use Kirchhoff's Laws to analyze circuits with AC sources?

A: Absolutely! Kirchhoff's Laws apply to both DC and AC circuits. However, in AC circuits, you need to work with complex numbers to represent the voltages and currents, as they vary sinusoidally with time. But the underlying principles remain the same.

Q: What happens if my circuit has a component that isn't a resistor, capacitor, or inductor? Like a diode or transistor?

A: Kirchhoff's Laws still apply! You just need to model those components differently. Diodes and transistors have nonlinear voltage-current relationships. You'll often use simplified models (like assuming a diode is a short circuit when forward-biased and an open circuit when reverse-biased) or rely on circuit simulation software to handle the more complex behavior.